Verkle Tries

Verkle trees are an improvement over conventional Merkle tree structures. While conventional Merkle tree structures use cryptographic hashes to commit to an indexed set of values, verkle trees use vector commitments. This makes them highly space efficient in terms of proof size, resulting in better bandwidth efficiency for communication. Additionally, verkle trees have cheaper verification costs in terms of state proof messaging.These are extremely important factors in scaling cross chain messaging through state proofs. Verkle trees were introduced in this research work from 2018, they hold the keys to cheap and efficient state proof messaging.

The goal of this section is to provide a comprehensive understanding of Verkle trees, including their construction and how they can be used to scale blockchain communication, specifically in the context of Hyperbridge.

Comparing Verkle trees to Base 16 Merkle Patricia tree

Merkle Patricia trees are an improvement over Merkle trees that enable the verification of key-value pairs. While merkle trees are binary trees, the base 16 merkle patricia tree allows you to have nodes which can be arrays of 16 items. This creates a more efficient merkle tree in terms of depth and tree traversal. However, there is a drawback. A merkle proof of a node includes all its sibling nodes and all nodes in the path to the root. Merkle proofs from a merkle patricia tree, although still logarithmic in size relative to the number of items in the tree, can still be quite large, with a space complexity of $O(k\log_k n)$ where $k=16$ . To avoid sacrificing too much bandwidth efficiency, it appears that a 16 item branch is the maximum width we can use. Increasing the width of the branches would only result in larger proof sizes.

For some context, in the Merkle Patricia Tree below, the proof for Leaf 3 would contain hash4, hash5, hash1, and hash2. This is because they are sibling nodes along the path to the root hash.

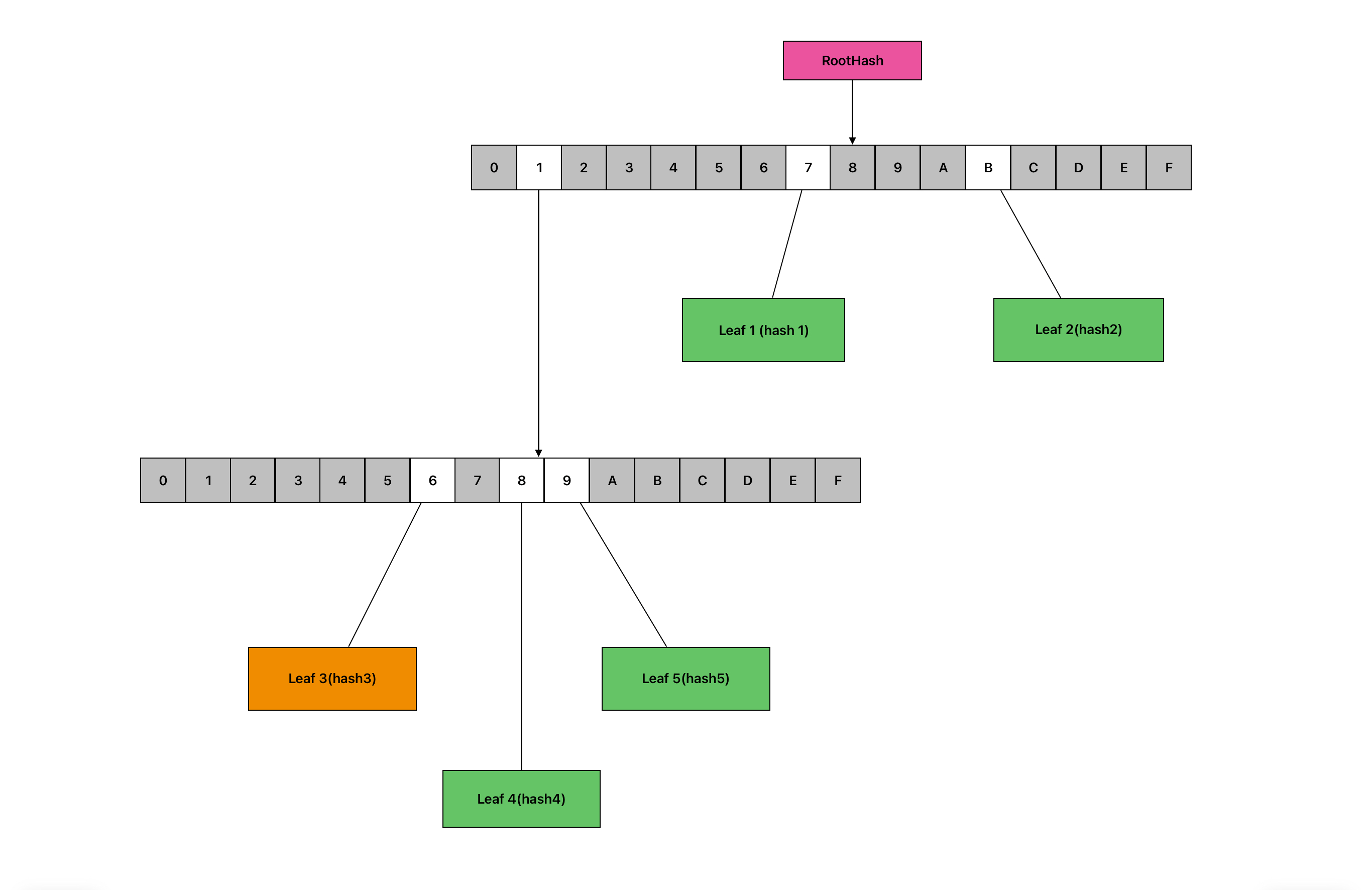
A Merkle Patricia Tree, empty nodes are shaded grey.

The main reason for the large size of merkle tree proofs is the use of a poor commitment scheme, cryptographic hashes. Verifying the hash requires us to reveal the full pre-image. Now, imagine if we could replace simple cryptographic hashes with a succinct cryptographic scheme that enables constant-sized commitments to a set of indexed values and allows verification of an item in the set without access to its siblings. This would significantly reduce proof size and enable the use of trees with very large widths. Vector commitments offer precisely these features. Verkle trees ensure that the proof size remains constant regardless of the tree width. Generating the proofs takes longer as the tree width increases, but we can choose an optimal width to balance reasonable proving times and benefit from proof sizes of $O(1)$ . According to benchmarks in the research paper, a width of 1024 offers the best balance of proving time and proof size.

Next let's define some standard equations.

The standard form for polynomials is given by the equation below :

\phi(x) = \sum_{i=0}^{l-1}\phi_ix^i\hspace{1cm}(1)

where $deg(\phi(x)) < l$ and $\phi_i$ are the coefficients of the polynomial.

A KZG commitment $C$ to a polynomial $\phi(x)$ is defined as:

C = \phi(\tau) = \prod_{i=0}^{l-1}(g^{\tau^i})^{\phi_i}\hspace{1cm}(2)

where $\tau$ is the secret key or trapdoor, $deg(\phi(x)) < l$ , $g$ is a generator of a pairing friendly elliptic curve group $\mathbb{G}$ , and $\phi_i$ are the coefficients of the polynomial.

If a polynomial $\phi(x)$ has an evaluation $\phi(z) = y$ , then there must exist a quotient polynomial $q(x)$ defined by:

q(x) = \frac {\phi(x) - y} {X-z}\hspace{1cm}(4)

where $(X-z)$ is a factor of $\phi(x)$

A KZG proof for the evaluation $\phi(z) = y$ for a polynomial $\phi(x)$ is defined as:

\pi = \phi(z) = \prod_{i=0}^{l-1}(g^{\tau^i})^{q_i}\hspace{1cm}(3)

where $\tau$ is the secret key or trapdoor, $deg(\phi(x)) < l$ , $g$ is a generator of a pairing friendly elliptic curve group $\mathbb{G}$ , and $q_i$ are the coefficients of the quotient polynomial.

Inserting Items

A tree can be described as a hierarchical structure that starts at a root node which branches out into child nodes. The number of child nodes a node can have is defined as the arity of the tree, a binary tree has an arity of 2. Let’s walkthrough how we can construct the tree in the diagram below.

The verkle tree described by the diagram below has the following properties:

A k-arity of 256.
Each node is indexed by a singe byte in the range 0x0..0xFF or 0..255 in decimal.
The keys in this tree are represented by a 32 byte hash.

Starting with an empty tree we’ll be inserting the following key value pairs in order:

(0xcea4070d609dd3497f72bde07fc96ba072763800a36a99fdfc7c10f6415f6ee6, 224) → Leaf A
(0xf0b46a0def9aa3497f72bde07fc96ba072763800a36a99fdfc7c10f6415f6ee6, 5330) → Leaf B
(0xceefd609dd3497f72bde07fc96ba05a9a74be4a5a7df60b01a6c0326c5e20, 2023) → Leaf C
(0xf0af65c3cf59d671eb72da0e7a4113c49f1f0515f462cdcf84e0f1d6045dfcbb, 1989) → Leaf D
(0xf0af9ecdc351df7acb72da0e7a4113c4bbd108c4899964f707fdaffb82636065, 2901) → Leaf E

Leaf A: The first byte of the key is 0xCE, so we store Leaf A at this index in the root node.

Leaf B: The first byte of the key is 0xF0, so we store Leaf B at this index in the root node.

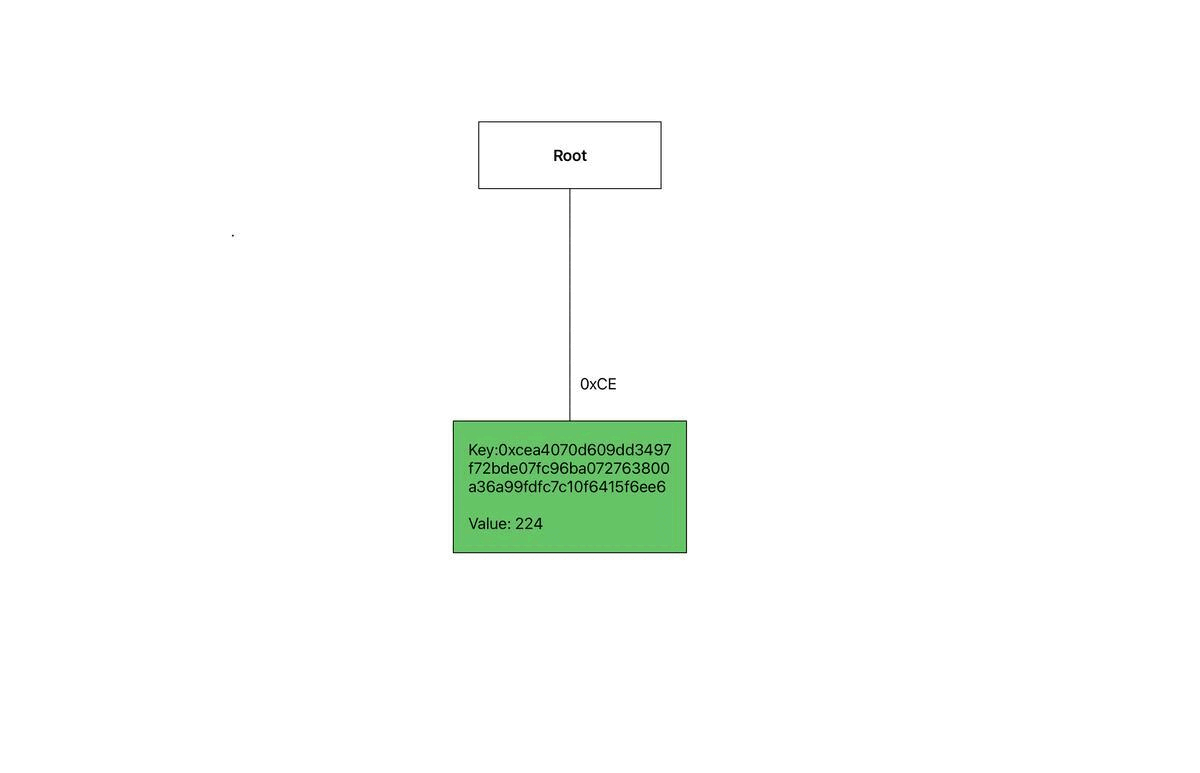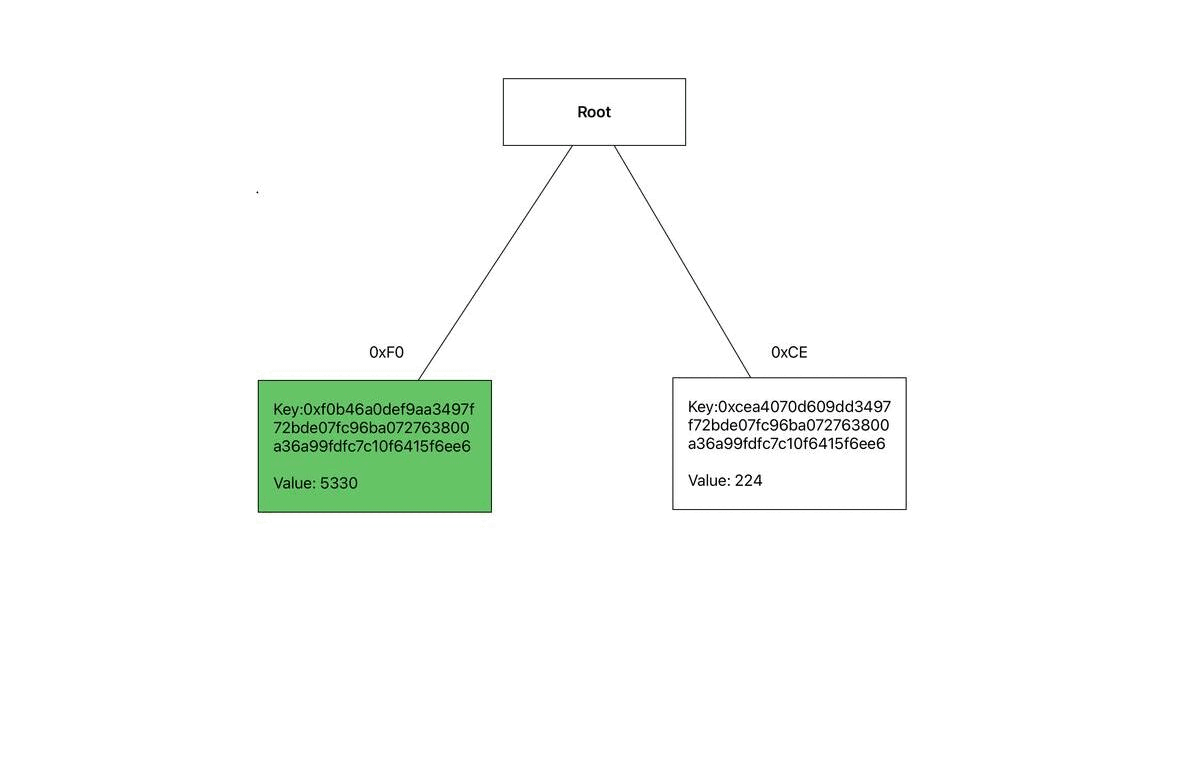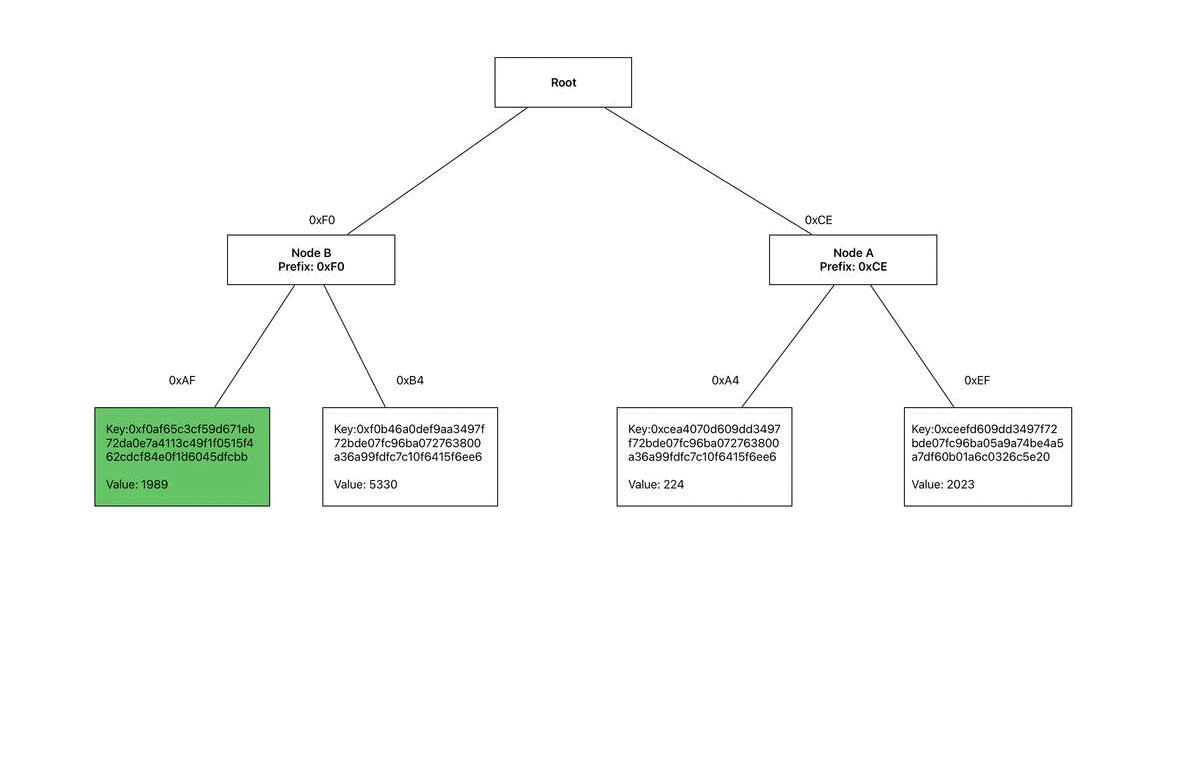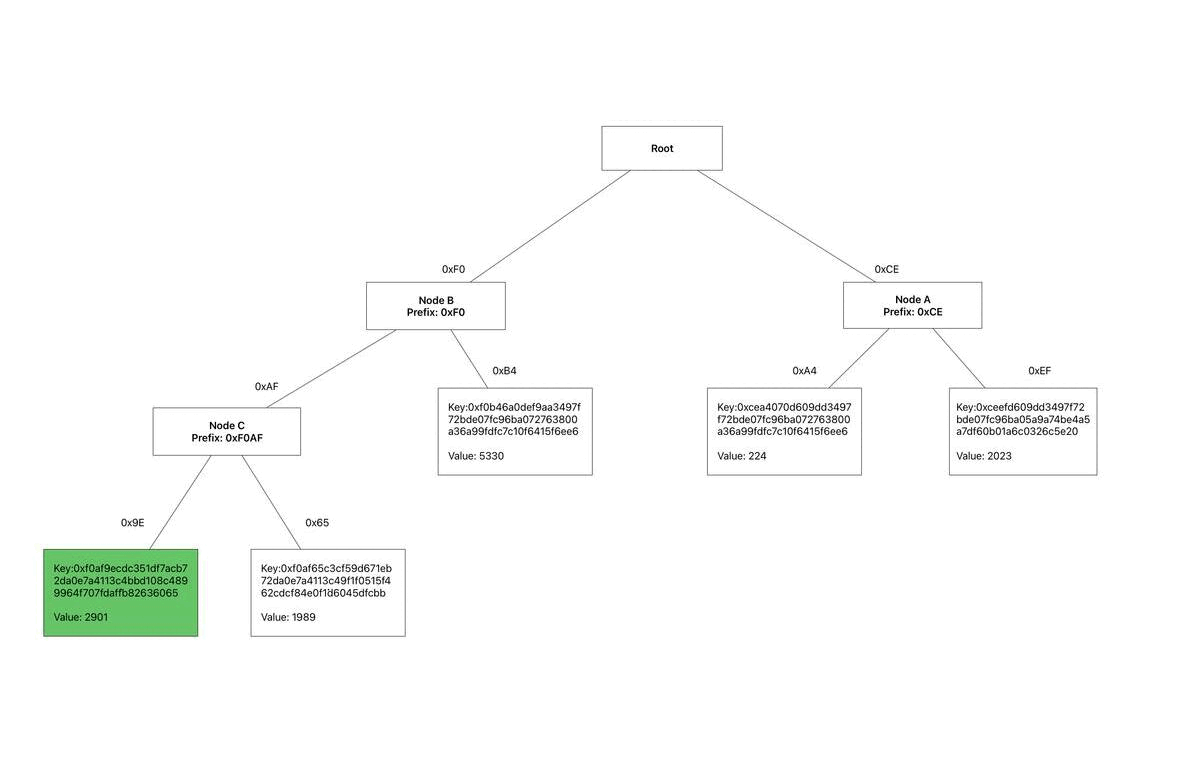
Leaf C: The first byte is 0xCE, so we remove the leaf stored at this index in the root node and insert a child node labeled Node A. We then store Leaf A and Leaf B at indices 0xA4 and 0xEF of this node.

Leaf D: The first byte is 0xF0, so we remove the leaf stored at this index in the root node and insert a child node labeled Node B. We then store Leaf B and Leaf D at indices 0xB4 and 0xAF of this node.

Leaf E: This key shares its first and second byte with Leaf D. Therefore, we remove Leaf D from index 0xAF of Node B and insert a child node labeled Node C. We then insert Leaf D and Leaf E at indices 0x65 and 0x9E of Node C.

A Gif showing how the tree grows as leaves are inserted

Committing changes to the tree

Committing changes to the tree involves computing the root commitment. We can obtain the root commitment by recursively computing the node commitments from the bottom of the tree until we reach the root node.

The value of each node that is not a leaf node is the hash of the polynomial commitment to its children.

To compute the commitment of a node in the tree, we hash the value stored at each index of the node. This gives us a list of hashes $[h_0...h_{k-1}]$ , for our specific tree $k = 256$ . We define a function $M$ that associates each hash in the list to a unique key in a finite field, such that we have a resulting list $[m_0,...,m_{k-1}]\in \mathbb{F_p}.$

Next, we interpolate over the points $[(m_0, h_0), ...,(m_{k-1}, h_{k-1})]$ to find the polynomial $\phi(x)$ with a degree $deg(\phi(x)) < k$ , such that $\phi(m_i)=h_i$ . This polynomial is then committed to, and the hash of this commitment is stored as the value of this node in its parent.

Ideally this process would be implemented with some caching so we are only recomputing commitments for nodes that were affected by a change(insertion or deletion) in the tree.

A simple verkle tree with k-arity of 256.

Verkle tree membership proofs

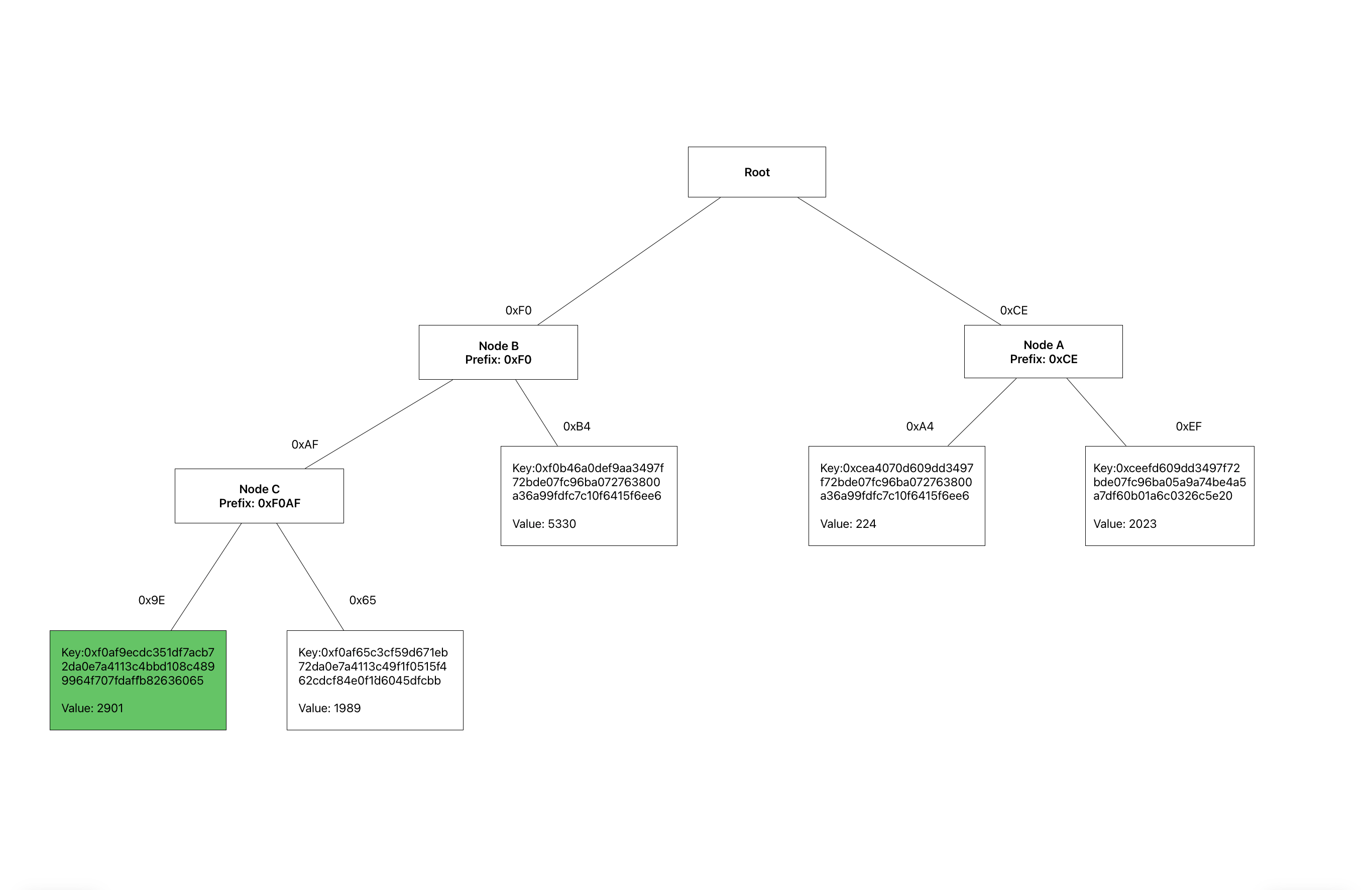
To prove the existence of a leaf in a verkle tree, The prover traverses the tree from the leaf to the root node and provides a commitment to each node, along with its corresponding KZG membership proof in its parent node. In the verkle tree described above let us have a hash function $H$ and the commitments to Node A and Node C be $C_1$ and $C_0$ respectively, our root commitment is defined as $C_r$ . To prove the existence of the leaf shaded green with key value pair (0xF0AF9ECDC351DF7ACB72DA0E7A4113C4BBD108C4899964F707FDAFFB82636065, 2901) the following is required:

The proof $\pi_0$ of the hash of the leaf $H($ 0xF0AF9ECDC351DF7ACB72DA0E7A4113C4BBD108C4899964F707FDAFFB82636065 $→ 2901)$ at index 0x9E in the commitment $C_0$ to Node C.
The proof $\pi_1$ of the hash $H(C_0)$ in the commitment $C_1$ to Node A at index 0xAF
The proof $\pi_2$ of hash $H(C_1)$ in the root commitment $C_r$ at index 0xF0

The prover provides the verifier with $\pi_0$ , $\pi_1$ , $\pi_2$ , $C_0$ , and $C_1$ to prove the existence of the leaf.

If we want to prove membership for multiple leaves using this approach, the number of intermediate KZG proofs will gradually increase as the key paths of the leaves diverge giving us overall proof sizes of $O(\log_k n)$ . In the next section, we will discuss how to combine all these proofs into a single KZG proof, which results in $O(1)$ proof size and improves bandwidth efficiency.

Verkle Tree batch proofs

A major benefit of KZG as a commitment scheme is its additive homomorphism property. This means that we can combine proofs for multiple polynomials opened at multiple points into a single proof. By doing so, we can amortize the costs of verifying large batches of items from the verkle tree. This section walks through how this can be achieved using random evaluation.

In the KZG scheme, the verifier requires the commitment to the polynomial being evaluated in order to verify a proof. Since the tree grows dynamically, the verifier only needs to maintain a commitment to the root node. Therefore, the prover must send the commitment to each intermediate node along the path from the leaf to the root. This cannot be avoided. However, we can optimize the process by merging all the intermediate membership proofs for these nodes into a single proof.

Consider some polynomials $\phi_0,...\phi_{t-1}$ and some evaluations of these polynomials $y_0,...,y_{t-1}$ at points $z_0,...z_{t-1}$ , from the fundamentals of algebra we know there exist quotient polynomials for each of those evaluations $q_0,...,q_{t-1}$ .

Our quotients are defined by (4). Since our quotients are meant to be polynomials, the summation of these quotients should also be a polynomial and not a rational function. A rational function is an algebraic fraction with both the numerator and denominator as algebraic expressions.

Before summing, each quotient is multiplied by a random scalar $\gamma^i$ where $\gamma=H(C_0...C_{t-1}, y_0...y_{t-1}, z_0...z_{t-1})$ , $H$ is a hash function. Since $\gamma$ is chosen after the prover has committed to the input values, the prover cannot manipulate the resulting polynomial. Additionally, the multiplication by $\gamma$ ensures that the resulting polynomial $g(x)$ is not a polynomial resulting from remainder terms cancelling out each other. $g(x)$ is defined as:

g(x) = \gamma^0q_0+...+\gamma^{t-1}q_{t-1}

The prover provides us a commitment $B$ to $g(x)$ .

g(x) = \gamma^0\frac {\phi_0(x) - y_0} {X-z_0} +...+ \gamma^{t-1}\frac {\phi_{t-1}(x) - y_{t-1}} {X-z_{t-1}}\hspace{1cm}

g(x) = \sum_{i=0}^{t-1}\gamma^i\frac {\phi_i(x) - y_i} {X-z_i}

Now we can split into two terms

g(x) = \sum_{i=0}^{t-1}\gamma^i \frac {\phi_i(x)} {(X-z_i)} - \sum_{i=0}^{t-1}\gamma^i \frac {y_i} {(X-z_i)}

We can therefore have the following:

g_1(x) = \sum_{i=0}^{t-1}\gamma^i \frac {C_i} {(X-z_i)}

g_2(x) = \sum_{i=0}^{t-1}\gamma^i \frac {y_i} {(X-z_i)}

Where $C_i$ is the commitment to the polynomial $\phi_i(x)$ , remember that the prover provides the verifier with all required commitments.

Now we choose a random point $r$ at which to evaluate $g(x)$ , $r = H(\gamma, B)$ since $r$ is chosen after the prover has committed to the commitment $B$ it is impossible for the prover to trick the verifier with a malicious proof.

Rewriting the previous equations in terms of $r$ we have:

g_1(r) = \sum_{i=0}^{t-1}\gamma^i \frac {C_i} {(r-z_i)}

g_2(r) = \sum_{i=0}^{t-1}\gamma^i \frac {y_i} {(r-z_i)}

g(r) = g_1(r) - g_2(r)

Notice that the verifier can compute the value of $g_2(r)$ , let $g_2(r) = y$ and $h(x) = g_1(x)$ , we now rearrange the equation to have:

y = h(r) - g(r)

y = D - B

Now given commitments $D$ to $h(x)$ and $B$ to $g(x)$ , the prover provides us a proof of the opening commitment $D-B$ at $r$ , this proves that $g_2(r) = y$ .

From the KZG scheme this proof is defined as:

\pi = \frac {D - B - y} {\tau - r}

To verify this proof the verifier uses the asymmetric pairing check given by:

e({D - B - y}, G_2) = e(\pi, [\tau - r]_2)

A successful verification of this proof, means that the commitment $B$ which was opened at a random point $r$ which the prover did not know prior to committing to $g(x)$ is valid, this validates the claim that $g(x)$ is a polynomial.

Applying KZG Batch Proofs to a verkle tree

To prove the existence of the leaf shaded green and its sibling node in the Verkle tree described above:

Let the hashes of these leaves $h_0$ and $h_1$ respectively.
Let the hash of the commitment to Node C and Node B be $h_2$ and $h_3$ respectively.
The function $M$ is used to associate these hashes to unique keys in a finite field which provides the values $[m_0, m_1, m_2, m_3] \in \mathbb{F_p}$ .
The polynomial that represents Node C is defined as $\phi_c(x)$ , such that $\phi_c(m_0) = h_0$ and $\phi_c(m_1) = h_1$ .
The polynomial that represents Node B and the Root Node are defined as $\phi_b(x)$ and $\phi_R(x)$ respectively.
Let the quotients for the evaluations given as $\phi_c(m_0) = h_0$ , $\phi_c(m_1) = h_1$ , $\phi_b(m_2) = h_2$ , $\phi_R(m_3) = h_3$ be $q_0$ , $q_1$ , $q_2$ and $q_3$ .
Compute $g(x) = \gamma^0q_0 + \gamma^1q_1 + \gamma^2q_2+ \gamma^3q_3$ .

The prover provides the verifier with the following:

The two leaves
The commitment to Node C and **Node B (**the verifier already knows the Root Node commitment).
The commitment $B$ to the polynomial sum of quotients $g(x)$
The KZG proof $\pi$ of evaluation of $g(x)$ at a random point $r = H(\gamma, B)$

Non Membership multi proofs

Non-membership proofs are constructed in the exact same way as membership proofs. The only difference is that, at the point where the path to a key terminates, the prover must prove the presence of a null hash. This is possible because, when interpolating the polynomial to calculate the commitment to a node as discussed above, the prover uses the null hash to represent empty indices. Therefore, when proving non-membership for multiple keys, the prover provides a KZG proof that convinces the verifier that the values of the keys in question inside the tree are equal to the null hash.