Binary Merkle Trees

A Merkle tree is a powerful data structure that enables efficient verification of large amounts of data. Specifically, a Merkle tree can be seen as a cryptographic hash-function whose pre-image is a virtual tree. As such, the root node of this structure is cryptographically dependent on all internal data and its root hash can be used as a secure identity for the data stored in the tree.

Merkle trees are constructed by recusively hashing pairs of data blocks, referred to as "leaves" and then hashing the hashes of the data to create a tree structure.

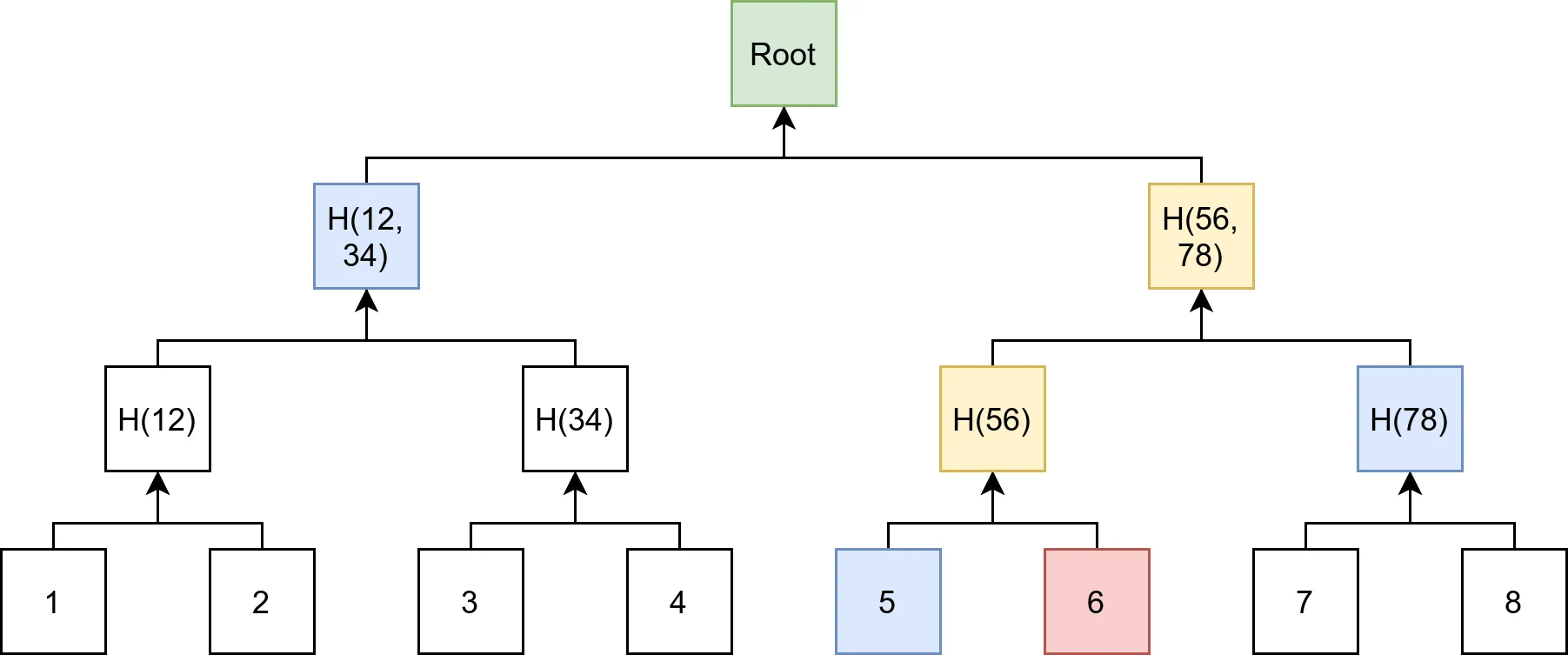
Properties

• The height of a Merkle tree is $h = log_2(n)$, where $n$ is the number of leaves in the tree.
• The number of leaves $n$ in a Merkle tree with a height $h$ is $n = 2^h$.
• The number of proof nodes for a single item proof is defined as $log_2(n_{leaves})$.
• The number nodes in a perfectly balanced, binary merkle tree with height $h$ is

Multi Proofs

Merkle multi proofs enable more efficient merkle proofs by re-using the intermediate nodes shared by the proof leaves during the recalculation of the root hash of the tree. In order to understand the benefits provided by merkle multi proofs, let’s look at the number of proof items needed for the green node in the tree below:

Proof schema for a single item in the tree. We need log₂(n) = 4 proof nodes.

Proof schema for another item in the merkle tree, which uses 3 proof nodes. (note: this tree is unbalanced)

A combined merkle multi proof uses only 5 proof nodes, in contrast to the total of 7 proof nodes required for verifying each node individually.

This scheme brings significant space savings when proving the existence of multiple items in a merkle tree. In this article, we introduce a custom proof format that gives us computational savings at the cost of additional space complexity for execution environments where the cost of execution may be too high.

We first define the $k$-index of any node in the tree as it’s distance to the leftmost node at every level of the tree:

Using this $k$-index. we can model the relationship between a parent node and it’s children nodes as:

$P_k = ⌊C_l^k / 2⌋ or ⌊C_r^k / 2⌋$

$C_l^k = 2(P_k)$

$C_r^k = 2(P_k) + 1$

Where:

$C_l^k = k$-index of left child node.

$C_r^k = k$-index of right child node.

$P_k = k$-index of parent node.

With the knowledge of the $k$-index of each node and its relationship with it’s parent, we can position the nodes in each layer sorted by this $k$-index to perform the correct hashing procedure needed to arrive at the parent node and it’s $k$-index for the next layer. We repeat this procedure until we reach the root node.

We can define our proof schema as a 2-dimensional array, where the first dimension encodes the layers of the tree, and the second dimension holds the proof nodes for that layer:

Second Pre-image Attacks

Second pre-image attacks arise when merkle tree proof schemes do not check the tree depth when verifying merkle proofs. This allows for attackers to construct either arbitrarily deep or shallow trees that have the same root hash as the verifier’s, in order to fool the verifier that some forged items are in the original tree.

In order to mitigate this, given our current proof scheme, it is necessary that the verifier knows the number of items in the tree. The height of the tree can be computed from it's leaf count and compared to the length of the 2D proof array (which encodes the height of the tree). If they do not match then the proof can safely be rejected because it describes a different tree and is attempting to perform a pre-image collision attack.

Verification Algorithm

Given this proof schema, The algorithm to calculate the root hash from a multi-proof is as follows:

\begin{algorithm}
\caption{Calculate Merkle Root from Multi-Proof}
\begin{algorithmic}
\INPUT  Leaves (a vector of nodes), Proof (a vector of vectors of nodes)
\OUTPUT Hash (a 32-byte array)
\PROCEDURE{CalculateMerkleRoot}{$leaves, proof$}
\State $\text{next\_layer} \gets []$
\State $\text{proof}[0] \gets \text{proof}[0] \cup \text{leaves}$
\State $\text{proof}[0] \gets \text{sort}(\text{proof}[0], \lambda a, b : a.k\_index < b.k\_index)$
\For{$\text{layer} \in \text{proof}$}
\State $\text{current\_layer} \gets []$
\If{$\text{next\_layer}.\text{length} = 0$}
\State $\text{current\_layer} \gets \text{layer}$
\Else
\State $\text{current\_layer} \gets \text{next\_layer} \cup \text{layer}$
\State $\text{current\_layer} \gets \text{sort}(\text{current\_layer}, \lambda a, b : a.k\_index < b.k\_index)$
\EndIf
\For{$\text{index} = 0; \text{index} < \text{current\_layer}.\text{length}; \text{index} += 2$}
\If{$\text{index} + 1 \geq \text{current\_layer}.\text{length}$}
\State $\text{node} \gets \text{current\_layer}[\text{index}]$
\State $\text{node}.k\_index \gets \text{node}.k\_index \div 2$
\State $\text{next\_layer}.\text{push}(\text{node})$
\Else
\State $\text{left} \gets \text{current\_layer}[\text{index}]$
\State $\text{right} \gets \text{current\_layer}[\text{index} + 1]$
\State $\text{concat} \gets \text{left}.node \cup \text{right}.node$
\State $\text{hash} \gets \text{hash}(\text{concat})$
\State $\text{parent} \gets \text{Node(}\text{k\_index} = \text{left}.k\_index \div 2, \text{node} = \text{hash)}$
\State $\text{next\_layer}.\text{push}(\text{parent})$
\EndIf
\EndFor
\EndFor
\State $\text{assert}(\text{next\_layer}.\text{length} = 1)$
\State \Return $\text{next\_layer}[0].\text{node}$
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

Implementation

You can find the implementation of this verification algiorithm in

• polytope-labs/solidity-merkle-trees