APK Proofs

Consensus proofs consist of signatures from a supermajority subset of the entire validator set. This can result in the cost of verifying consensus proofs scaling linearly with the size of the validator set. However, the BLS signature scheme overcomes this limitation by enabling the aggregation of signatures and public keys, reducing verifier complexity to a single pairing check. Unfortunately, this comes at the cost of being unable to confirm the identity of each individual signer. The apk proofs $^{[1]}$ scheme reintroduces accountability in this regard at the extra cost of verification of a single SNARK proof.

The SNARK achieves this by constraining the elliptic curve addition of BLS public keys in order to produce a proof that a given aggregate public key is the result of the aggregation of a subset of a known set. You can see how this is useful for consensus proofs produced by a known validator set in POS consensus. This is done with the aid of half-cycles of elliptic curves. These half-cycles allow for embedding the field elements of an inner curve (which represents the public keys) within the scalar field of the outer curve. Where you can do polynomial commitments and opening proofs for the SNARK proof. Cycles of curves were first introduced for the purpose of recursive SNARK proof verification.

Preliminaries

I refer to the inner curve which is the native curve of the public keys as $E_{inn}$ . For an elliptic curve half-cycle, it should be the case that the characteristic of the base field of the inner curve $E_{inn}(\mathbb{F}_p)$ is the same as the scalar field of the outer curve $E_{out}(\mathbb{F}_r)$ . Let $H$ be a suitably chosen multiplicative subgroup in the scalar field of the outer curve $E_{out}(\mathbb{F}_r)$ .

Protocol

First we need to arithmetise elliptic curve point addition. Recall the elliptic curve addition formula $P+ Q = R$ for a short weierstrass curve, The slope $\lambda$ between the two points is given as

\lambda = \frac{y_2-y_1}{x_2-x_1}

Such that:

\begin{split} x_3 &= \lambda^2 - x_1 - x_2 \\ y_3 &= \lambda(x_1-x_3) - y_1 \end{split}

Substituting $\lambda$ we get

\begin{split} x_3 = (\frac{y_2-y_1}{x_2-x_1})^2 - x_1 - x_2 \\ x_1 + x_2 +x_3 = (\frac{y_2-y_1}{x_2-x_1})^2 \\ (x_1 + x_2 +x_3)(x_2 - x_1)^2 - (y_2-y_1)^2 = 0 \end{split}

In the same manner, we constrain the value for $y_3$

\begin{split} y_3 = (\frac{y_2-y_1}{x_2-x_1})(x_1-x_3) - y_1 \\ y_1 + y_3 = \frac{y_2-y_1}{x_2-x_1} \cdot (x_1-x_3)\\ (y_1 + y_3)(x_2-x_1) - (y_2-y_1)(x_1-x_3) = 0 \end{split}

The goal is to show that $apk = \sum^{n-1}_{i=0} pk_i \cdot b_i$ , where $pk$ is a vector of known public keys and $b$ is a bitvector indicating the signers. We’ll do so by means of an accumulator. Observe that we can write

(kaccx_{i+1}, kaccy_{i + 1}) = (kaccx_{i}, kaccy_{i}) \oplus b_i \cdot (pkx_i, pky_i)

Where $pk\{x,y\}$ are the affine coordinates of the potential signers and $kacc\{x,y\}$ is the accumulator sum.

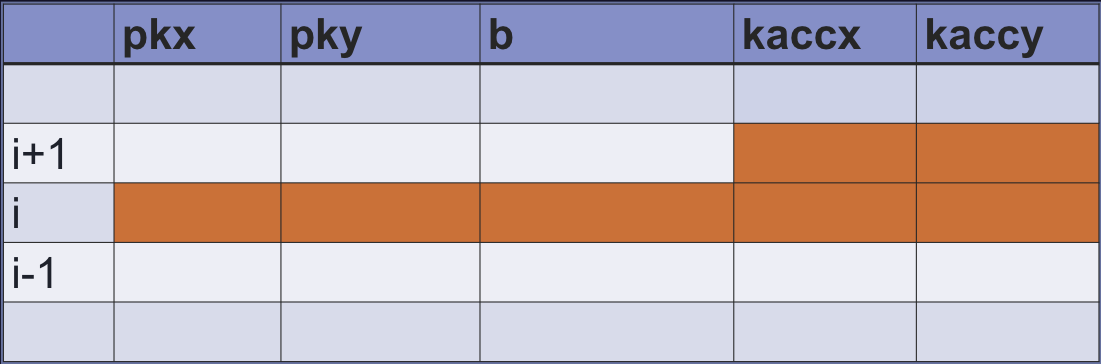
APK Proof Circuit

constraining with $b$ we get:

b((y_2-y_1)^2 - (x_1 + x_2 +x_3)(x_2 - x_1)^2) + (1-b)(y_3 - y_1) = 0 \\ b((y_2-y_1)(x_1-x_3) - (y_1 + y_3)(x_2-x_1)) + (1-b)(x_3-x_1) = 0

Lifting these equations to polynomial constraints:

\begin{split} id_1(X) &= (X-\omega^{n-1})(b(X)((pky(X)-kaccy(X))^2 - (kaccx(X) + pkx(X) + kaccx(\omega \cdot X))(pkx(X) - kaccx(X))^2) + (1-b(X))(kaccy(\omega \cdot X) - kaccy(X))) \\ id_2(X) &= (X-\omega^{n-1})(b(X)((pky(X)-kaccy(X))(kaccx(X)-kaccx(\omega \cdot X)) - (kaccy(X) + kaccy(\omega \cdot X))(pkx(X)-kaccx(X))) + (1-b(X))(kaccx(\omega \cdot X)- kaccx(X))) \end{split}

Where

\begin{split} pkx(X) &= \mathcal{L}_i(X) \cdot pkx_i \\ pky(X) &= \mathcal{L}_i(X) \cdot pky_i \\ kaccx(X) &= \mathcal{L}_i(X) \cdot kaccx_i \\ kaccy(X) &= \mathcal{L}_i(X) \cdot kaccy_i \\ b(X) &= \mathcal{L}_i(X) \cdot b_i \\ \end{split}

Assume $\mathcal{L}_i(X)$ are Lagrange polynomials in the domain $H$ . The verifier has commitments to $C_{pkx}$ and $C_{pky}$ . They’ll receive the commitments and opening proofs for the polynomials, $C_{kaccx}, C_{kaccy}$ and $C_b$ . Which allows them to check the above polynomial constraints. Next we need to constrain the circuit inputs. We initialise the accumulator with a chosen point $h \in \mathbb{E}_{inn}$ . Such that:

(kaccx_0, kaccy_0) = (h_x, h_y) \\ (kaccx_{n-1}, kaccy_{n-1}) = (apk_x, apk_y) \oplus (h_x, h_y)

We’ll constrain using these equations.

(kaccx_0 - h_x) + (kaccx_{n-1} - (apk_x + h_x)) = 0 \\ (kaccy_0 - h_y) + (kaccy_{n-1} - (apk_y + h_y)) = 0

Lifting to polynomial constraints

id_3(X) = \mathcal{L}_0(X)(kaccx(X) - h_x) + \mathcal{L}_{n-1} (kaccx(X) - (apk_x + h_x)) \\ id_4(X) = \mathcal{L}_0(X)(kaccy(X) - h_y) + \mathcal{L}_{n-1} (kaccy(X) - (apk_y + h_y))

Finally the prover has to show that each $b_i \in \{0, 1\}$ . They’ll do so using the polynomial constraint

id_5(X) = b(X)(1 - b(X))

In the Basic Accountable scheme, the bitvector is represented using individual field elements of the inner curve. This can be particularly expensive. In order to reduce space complexity of the bitlist and produce proofs of larger sets, it becomes necessary for the prover to represent the signers using the binary representation of each field element. This is more compact and saves significant communication complexity when dealing with signers of size $2^{20}$ and above.

The paper introduces two new polynomials in it’s Packed Accountable Ranged scheme. First we must understand that any number $z$ can be re-written as an inner product of its binary representation and powers of 2. This also known as binary decomposition.

\begin{split} z &= \langle2^i, z_i \rangle \\ &= \sum^{n -1}_{i = 0} 2^i \cdot z_i \\ \end{split}

First we define $block$ as the maximum number of bits in the binary representation in the field element we’ll use to represent chunks of our bitlist. The verifier can simply check that the pre-approved number of bits are used on in each of the field elements provided by the prover.

0 \le countOnes(b^\prime) < block

In order to use binary decomposition tricks, it’s necessary $block$ is a power of 2. ie $block = 2^k < n$ . Rather than a bitlist, the prover provides a vector of field elements $b^\prime$

\begin{split} b^\prime &= (b^\prime_0, \dots, b^\prime_{\frac{n}{block} - 1})\\ \end{split}

where each $b^\prime_j \in E_{inn}(\mathbb{F}_p)$ can be seen as

b^\prime_j = \sum^{block - 1}_{i = 0} 2^i \cdot b_{(block \cdot j) + i}

The verifier wants to know that the bitlist encoded in the binary representation of $b^\prime$ is equal to $b(X)$ . We do so by means of a range proof. Observe that

\begin{split} sum &= \sum^{\frac{n}{block} - 1}_{j = 0} b^\prime_j \cdot r^j \\ &= \sum^{\frac{n}{block} - 1}_{j = 0} (\sum^{block - 1}_{i = 0} 2^i \cdot b_{(block \cdot j) + i} ) \cdot r^j \\ &= \sum^{n - 1}_{i = 0} 2^{i \mod{block}} \cdot b_i \cdot r^{i \div block} \end{split}

We begin by decomposing the final equation. First lets define a selector polynomial $aux(X)$

aux(X) = \sum^{n - 1}_{i = 0} aux_i \cdot \mathcal{L}_i(X)

Where $aux_i$ is given as

aux_i = \begin{cases} 1 & i \mid block \\ 0 & i \nmid block \end{cases}

Note that 0 is divisible by any $x$ . Next we define

c_a(X) = \sum^{n - 1}_{i = 0} c_{a,i} \cdot \mathcal{L}_i(X)

Where

c_{a,i} = 2^{i \mod{block}} \cdot r^{\frac{i}{block}}

The prover must then show that the following polynomial is zero over $H$

\begin{split} id_{6}(X) = c_a(\omega \cdot X) - c_a(X) \cdot (2 + (\frac{r}{2^{block - 1}} - 2) \cdot aux(\omega \cdot X)) - (1 - r^{\frac{n}{block}}) \cdot \mathcal{L}_{n-1}(X) \end{split}

Lets consider the case when $i \nmid block$ , we have that:

\begin{split} id_{6}(\omega^i) &= c_a(\omega \cdot \omega^i) - (c_a(\omega^i) \cdot 2) \\ &= (2^{(i \mod{block}) + 1} \cdot r^{\frac{i}{block}}) - ((2^{i \mod{block}} \cdot r^{\frac{i}{block}}) \cdot 2) \\ &= r^{\frac{i}{block}}(2^{(i \mod{block}) + 1} - 2^{(i \mod{block}) + 1}) \\ \end{split}

Lets consider the second case when $i \mid block$ , we have that:

\begin{split} id_{6}(\omega^i) &= c_a(\omega \cdot \omega^i) - c_a(\omega^i) \cdot (2 + (\frac{r}{2^{block - 1}} - 2)) \cdot 1 \\ &= (2^0 \cdot r^{(\frac{i}{block}) + 1}) - (2^{block - 1} \cdot r^{\frac{i}{block}}) \cdot (\frac{r}{2^{block - 1}}) \\ &= r^{(\frac{i}{block}) + 1} - r^{(\frac{i}{block}) + 1} \end{split}

Finally lets consider the case where $i = n-1$ , It’s easy to see that $c_{a,0} = 1$ . Therefore

\begin{split} id_{6}(\omega^{n-1}) &= 1 - (2^{block-1} \cdot r^{\frac{n}{block} - 1}) \cdot (2 + (\frac{r}{2^{block - 1}} - 2) \cdot 1) - (1 - r^{\frac{n}{block}}) \cdot 1 \\ &= (1 - r^{\frac{n}{block} - 1} \cdot r) - (1 - r^{\frac{n}{block}}) \\ &= (1 - r^{\frac{n}{block}}) - (1 - r^{\frac{n}{block}}) \end{split}

The polynomial $id_6(X)$ constrains the form of $c_{a_i} \in [0, (2^{i \mod{block}} \cdot r^{\frac{i}{block}})] \forall i \in [0, n-1)$ . Next we introduce an accumulator polynomial for $c_{a, i}$ .

acc_a(X) = acc_{a, i} \cdot \mathcal{L}_i(X)

where $acc_{a, i}$ are the components of the vector:

[0, bit_i \cdot c_{a, 0}, (bit_0 \cdot c_{a,0}) + (bit_1 \cdot c_{a,1}), \dots, \sum^{n-2}_{i = 0}(bit_i \cdot c_{a, i})]

The prover must show that the following polynomial evaluates to zero over $H$

\begin{split} id_7(X) = acc_a(\omega \cdot X) - acc_a(X) - (b(X) \cdot c_a(X)) + sum \cdot \mathcal{L}_{n-1}(X) \end{split}

Observe that

\begin{split} acc_a(\omega \cdot X) - acc_a(X) &= bit_i \cdot c_{a, i} \\ &= b(X) \cdot c_a(X) \end{split}

Therefore

\begin{split} id_7(\omega^i) = (b(\omega^i) \cdot c_a(\omega^i)) - (b(\omega^i) \cdot c_a(\omega^i)) \end{split}

Considering the case when $i =n-1$

\begin{split} id_7(\omega^{n-1}) &= 0 - (\sum^{n-2}_{i = 0}(bit_i \cdot c_{a, i})) - (b(\omega^{n-1}) \cdot c_a(\omega^{n-1})) + sum \cdot 1 \\ &= -sum + sum \end{split}

This convinces the verifier that $b(X)$ is equivalent to $b^\prime$ . Finally the apk proof constraint polynomial $t(X)$ is given as:

\begin{split} t(X)(X^n-1) &= id_1(X)(X- \omega^{n-1}) + \alpha \cdot id_2(X)(X-\omega^{n-1}) + \alpha^2 \cdot id_3(X) + \alpha^3 \cdot id_4(X) + \alpha^4 \cdot id_5(X)+ \alpha^5 \cdot id_6(X)+ \alpha^6 \cdot id_7(X) \\ \end{split}

Or in expanded form

\begin{split} t(X)(X^n-1) &= (X-\omega^{n-1})(b(X)((pky(X)-kaccy(X))^2 - (kaccx(X) + pkx(X) + kaccx(\omega \cdot X))(pkx(X) - kaccx(X))^2) + (1-b(X))(kaccy(\omega \cdot X) - kaccy(X))) \\ &+ \alpha (X-\omega^{n-1}) \cdot [b(X)((pky(X)-kaccy(X))(kaccx(X)-kaccx(\omega \cdot X)) - (kaccy(X) + kaccy(\omega \cdot X))(pkx(X)-kaccx(X))) + (1-b(X))(kaccx(\omega \cdot X)- kaccx(X)) ] \\ &+ \alpha^2 \cdot [\mathcal{L}_0(X)(kaccx(X) - h_x) + \mathcal{L}_{n-1} (kaccx(X) - (apk_x + h_x)) ] \\ &+ \alpha^3 \cdot [\mathcal{L}_0(X)(kaccy(X) - h_y) + \mathcal{L}_{n-1} (kaccy(X) - (apk_y + h_y)) ] \\ &+ \alpha^4 \cdot [b(X)(1 - b(X))] \\ &+ \alpha^5 \cdot [c_a(\omega \cdot X) - c_a(X) \cdot (2 + (\frac{r}{2^{block - 1}} - 2) \cdot aux(\omega \cdot X)) - (1 - r^{\frac{n}{block}}) \cdot \mathcal{L}_{n-1}(X)] \\ &+ \alpha^6 \cdot [acc_a(\omega \cdot X) - acc_a(X) - (b(X) \cdot c_a(X)) + sum \cdot \mathcal{L}_{n-1}(X)] \\ \end{split}

Where $\alpha \in E_{out}(\mathbb{F}_r)$ is a value chosen by the verifier. Given this constraint polynomial, it’s trivial to lift this further into SNARK using the PLONK protocol or any of it’s variants.

References

$^{[1]}$ Accountable Light Client Systems for PoS Blockchains, Oana Ciobotaru, Fatemeh Shirazi, Alistair Stewart, and Sergey Vasilyev.