Skip to content

Merkle Patricia Trie

Patricia Trie

A PATRICIA Trie[1]^{[1]}, also known as a radix trie, is a kind of kk-ary search tree which is used for efficiently looking up items in a database. It achieves an O(logkn)O(log_kn) search complexity by encoding the keys in the trie nodes along the path to the data. Unlike conventional tries, a Patricia trie only creates a node for each unique prefix of its keys. This reduces the amount of memory required to store the trie and allows for faster lookups.

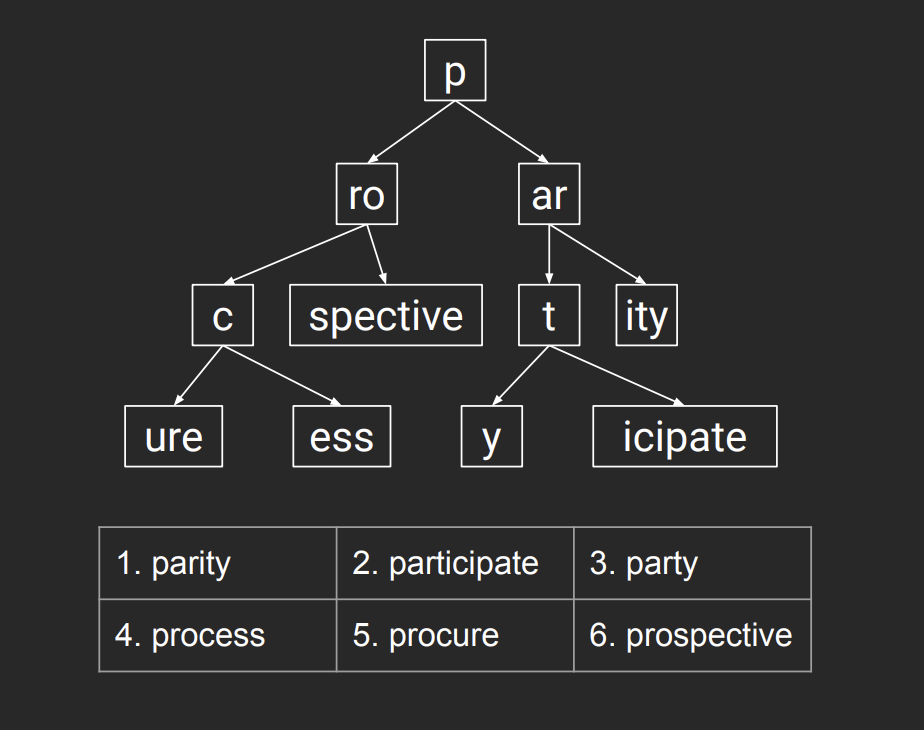
An example of a binary PATRICIA trie
An example of a binary PATRICIA trie.

Patricia tries were first described by Donald R. Morrison in 1968 and have since been used in a variety of applications, including IP routing tables and spell checkers. They are a powerful data structure that can greatly improve the efficiency of searching and retrieving data from large databases.

Merkle-Patricia Trie

The Merkle-Patricia trie was invented by Dr. Gavin Wood, co-founder of Ethereum. It was first described in the Ethereum yellow paper[2]^{[2]}. This data structure combines the PATRICIA and Merkle trees into a single tree, which has the ability to store key-value items while still allowing for O(klogkn)O(klog_kn) merkle proofs. Where, kk represents the arity of each node and nn represents the number of leaves in the tree. The yellow paper prescribes an arity of 16, but using other arities is also possible.

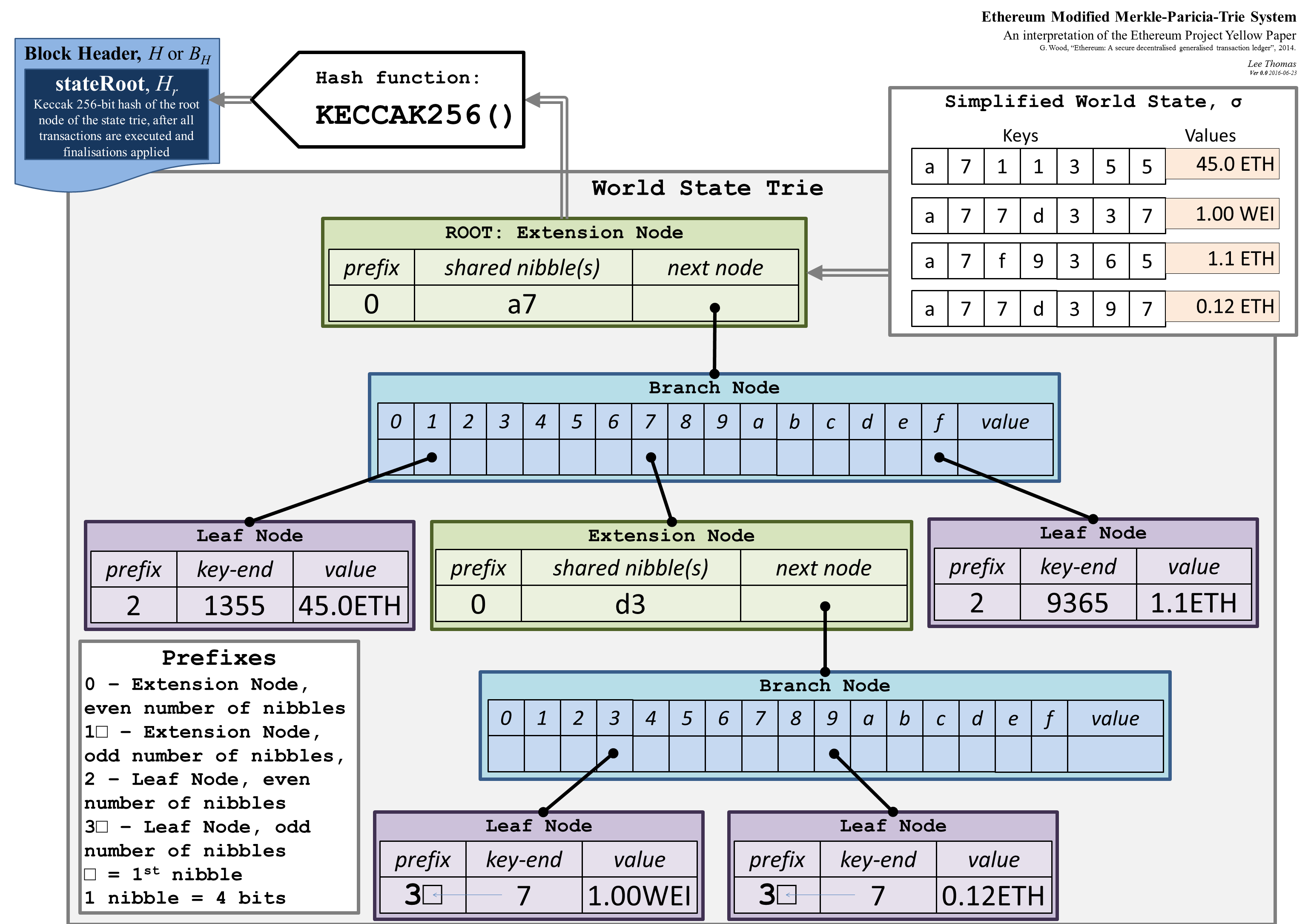
trie world.png

The yellow paper describes 3 kinds of Merkle-Patricia nodes:

Leaf Nodes

Untitled Diagram (2).svg

A leaf node can be thought of a 2-item tuple, whose first item corresponds to the bytes in the key not already accounted for by the accumulation of keys in the branch & extension nodes traversed from the root. The second item corresponds to the actual value held at the leaf node. The hash of a leaf node is gotten by concatenating it’s partial key with the hash of it’s value and taking the hash of this concatenation.

Extension Nodes

extension.svg

An extension node serves as a key accumulation node for keys that would’ve otherwise been encoded into deeply nested branch nodes. Much like the leaf node it is a 2-item tuple, it’s first item hold the key bytes shared by its child node, but its second item points to another (usually a branch) node in the trie. The hash of an extension node is gotten by concatenating it’s partial key with the hash of it’s child node and taking the hash of this concatenation.

Branch Nodes

branch.svg

A branch node on the other hand is a 17-item tuple, where the first 16 items in the tuple correspond to all the possible nibble (242^4 or half a byte) values which hold the hash of a node at those positions, while the 17th item holds a possible value. The hash of a branch node is gotten by concatenating of the hash of all its children nodes and taking the hash of this concatenation. This is also the reason why the merkle-patricia trie has O(klogkn)O(klog_kn) merkle proofs, as you’d need to include the hash of all sibling nodes in all the branch nodes along the path to the leaf node.

Compact Merkle Patricia Proofs

NibbledBranch.svg

The merkle-patricia trie was further modified for substrate and polkadot, resulting in more compact state proofs by eliminating extension nodes[3]^{[3]}. Instead, partial keys were introduced to branch nodes. This means that branch nodes can hold accumulated partial keys, which eliminates the need for a dedicated extension node. With this modification state proofs are effectively compacted and less nodes are required in state proofs.

Algorithms

We give the following algorithms for verifying Merkle Patricia Trie proofs:

Substrate/Polkadot

\begin{algorithm}
\caption{Verify Substrate Proof}
\begin{algorithmic}
\PROCEDURE{VerifySubstrateProof}{$\text{root}, \text{proof}, \text{keys}$}
\State $\text{values} \gets \text{array of StorageValue of length } \text{length}(\text{keys})$
\State $\text{nodes} \gets \text{array of TrieNode of length } \text{length}(\text{proof})$

\For{$i = 0$ \textbf{to} $\text{length}(\text{proof}) - 1$}
\State $\text{nodes}[i] \gets \text{TrieNode}(\text{keccak256}(\text{proof}[i]), \text{proof}[i])$
\EndFor

\For{$i = 0$ \textbf{to} $\text{length}(\text{keys}) - 1$}
\State $\text{values}[i].\text{key} \gets \text{keys}[i]$
\State $\text{keyNibbles} \gets \text{NibbleSlice}(\text{keys}[i], 0)$
\State $\text{node} \gets \text{SubstrateTrieDB.decodeNodeKind}(\text{TrieDB.get}(\text{nodes}, \text{root}))$

\For{$j = 1$ \textbf{to} $\infty$}
\State $\text{nextNode} \gets \text{undefined}$
\If{$\text{TrieDB.isLeaf}(\text{node})$}
\State $\text{leaf} \gets \text{SubstrateTrieDB.decodeLeaf}(\text{node})$
\If{$\text{NibbleSliceOps.eq}(\text{leaf.key}, \text{keyNibbles})$}
\State $\text{values}[i].\text{value} \gets \text{TrieDB.load}(\text{nodes}, \text{leaf.value})$
\EndIf
\State \textbf{break}
\ElsIf{$\text{TrieDB.isNibbledBranch}(\text{node})$}
\State $\text{nibbled} \gets \text{SubstrateTrieDB.decodeNibbledBranch}(\text{node})$
\State $\text{nibbledBranchKeyLength} \gets \text{NibbleSliceOps.len}(\text{nibbled.key})$
\If{not $\text{NibbleSliceOps.startsWith}(\text{keyNibbles}, \text{nibbled.key})$}
\State \textbf{break}
\EndIf
\If{$\text{NibbleSliceOps.len}(\text{keyNibbles}) = \text{nibbledBranchKeyLength}$}
\If{$\text{Option.isSome}(\text{nibbled.value})$}
\State $\text{values}[i].\text{value} \gets \text{TrieDB.load}(\text{nodes}, \text{nibbled.value.value})$
\EndIf
\State \textbf{break}
\Else
\State $\text{index} \gets \text{NibbleSliceOps.at}(\text{keyNibbles}, \text{nibbledBranchKeyLength})$
\State $\text{handle} \gets \text{nibbled.children}[\text{index}]$
\If{$\text{Option.isSome}(\text{handle})$}
\State $\text{keyNibbles} \gets \text{NibbleSliceOps.mid}(\text{keyNibbles}, \text{nibbledBranchKeyLength} + 1)$
\State $\text{nextNode} \gets \text{handle.value}$
\Else
\State \textbf{break}
\EndIf
\EndIf
\ElsIf{$\text{TrieDB.isEmpty}(\text{node})$}
\State \textbf{break}
\EndIf
\State $\text{node} \gets \text{SubstrateTrieDB.decodeNodeKind}(\text{TrieDB.load}(\text{nodes}, \text{nextNode}))$
\EndFor
\EndFor
\State \Return $\text{values}$
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

Ethereum

\begin{algorithm}
\caption{Verify Ethereum Proof}
\begin{algorithmic}
\PROCEDURE{VerifyEthereumProof}{$\text{root}, \text{proof}, \text{keys}$}
\State $\text{values} \gets \text{array of StorageValue of length } \text{length}(\text{keys})$
\State $\text{nodes} \gets \text{array of TrieNode of length } \text{length}(\text{proof})$

\For{$i = 0$ \textbf{to} $\text{length}(\text{proof}) - 1$}
\State $\text{nodes}[i] \gets \text{TrieNode}(\text{keccak256}(\text{proof}[i]), \text{proof}[i])$
\EndFor

\For{$i = 0$ \textbf{to} $\text{length}(\text{keys}) - 1$}
\State $\text{values}[i].\text{key} \gets \text{keys}[i]$
\State $\text{keyNibbles} \gets \text{NibbleSlice}(\text{keys}[i], 0)$
\State $\text{node} \gets \text{EthereumTrieDB.decodeNodeKind}(\text{TrieDB.get}(\text{nodes}, \text{root}))$

\For{$j = 1$ \textbf{to} $\infty$}
\State $\text{nextNode} \gets \text{undefined}$
\If{$\text{TrieDB.isLeaf}(\text{node})$}
\State $\text{leaf} \gets \text{EthereumTrieDB.decodeLeaf}(\text{node})$
\State $\text{offset} \gets \text{keyNibbles.offset} \mod 2 = 0 \text{ ? } \text{keyNibbles.offset} / 2 : \text{keyNibbles.offset} / 2 + 1$
\State $\text{keyNibbles} \gets \text{NibbleSlice}(\text{NibbleSliceOps.bytesSlice}(\text{keyNibbles.data}, \text{offset}), 0)$
\If{$\text{NibbleSliceOps.eq}(\text{leaf.key}, \text{keyNibbles})$}
\State $\text{values}[i].\text{value} \gets \text{TrieDB.load}(\text{nodes}, \text{leaf.value})$
\EndIf
\State \textbf{break}
\ElsIf{$\text{TrieDB.isExtension}(\text{node})$}
\State $\text{extension} \gets \text{EthereumTrieDB.decodeExtension}(\text{node})$
\If{$\text{NibbleSliceOps.startsWith}(\text{keyNibbles}, \text{extension.key})$}
\State $\text{cutNibble} \gets \text{keyNibbles.offset} + \text{NibbleSliceOps.len}(\text{extension.key})$
\State $\text{keyNibbles} \gets \text{NibbleSlice}(\text{NibbleSliceOps.bytesSlice}(\text{keyNibbles.data}, \text{cutNibble} / 2), \text{cutNibble} \mod 2)$
\State $\text{nextNode} \gets \text{extension.node}$
\Else
\State \textbf{break}
\EndIf
\ElsIf{$\text{TrieDB.isBranch}(\text{node})$}
\State $\text{branch} \gets \text{EthereumTrieDB.decodeBranch}(\text{node})$
\If{$\text{NibbleSliceOps.isEmpty}(\text{keyNibbles})$}
\If{$\text{Option.isSome}(\text{branch.value})$}
\State $\text{values}[i].\text{value} \gets \text{TrieDB.load}(\text{nodes}, \text{branch.value.value})$
\EndIf
\State \textbf{break}
\Else
\State $\text{handle} \gets \text{branch.children}[\text{NibbleSliceOps.at}(\text{keyNibbles}, 0)]$
\If{$\text{Option.isSome}(\text{handle})$}
\State $\text{keyNibbles} \gets \text{NibbleSliceOps.mid}(\text{keyNibbles}, 1)$
\State $\text{nextNode} \gets \text{handle.value}$
\Else
\State \textbf{break}
\EndIf
\EndIf
\ElsIf{$\text{TrieDB.isEmpty}(\text{node})$}
\State \textbf{break}
\EndIf
\State $\text{node} \gets \text{EthereumTrieDB.decodeNodeKind}(\text{TrieDB.load}(\text{nodes}, \text{nextNode}))$
\EndFor
\EndFor

\State \Return $\text{values}$
\ENDPROCEDURE
\end{algorithmic}
\end{algorithm}

Implementations

You can find the implementation of this verification algiorithm in

References

[1]^{[1]} Morrison, Donald R. PATRICIA -- Practical Algorithm to Retrieve Information Coded in Alphanumeric

[2]^{[2]} G. Wood, Appendix D, Ethereum: A Secure Decentralized Generalized Transaction Ledger, 2015

[3]^{[3]} Polkadot Protocol Specification: 2.4.3 Trie Structure