zkCasper

Special thanks to Alistair Stewart, Oana Ciobotaru and Sergey Vasilyev (authors of the “Accountable Light Client Systems for PoS Blockchains” paper) for the helpful discussions and feedback that were instrumental in making this protocol possible.

We present a protocol for efficiently verifying the Ethereum Beacon chain's Casper FFG consensus proofs using a SNARK-based approach. With this scheme, computationally constrained environments, such as on-chain or off-chain consensus clients, can securely follow the Casper FFG protocol and benefit from the crypto-economic security provided by the over 17 million ETH ($34 billion at the time of writing) staked on the Beacon chain. This protocol offers full node-level security that is orders of magnitude more secure than the sync committee, and is fully Byzantine fault-tolerant.

Motivation

The sync committee was introduced to the beacon chain in the Altair hard-fork and it consists of a randomly selected subset of 512 validators from the full validator set. The motivation for this committee was consensus proofs that could be verified cheaply. Unfortunately, this protocol introduces new security assumptions that are completely orthogonal to the security of the beacon chain. More specifically, it has much lower crypto-economic security, as well as a lack of slashing for byzantine behavior, which is critical to the safety of POS consensus.

Therefore, bridges and off-chain consensus clients that rely on the beacon chain consensus proofs must trust that the sync committee will not collude to perform eclipse or data withholding attacks, even when there are no consequences for such actions. We find this blind-faith security model to be completely unacceptable. Consequently, we have opted for the more ambitious approach of directly verifying the Casper FFG consensus proofs.

Preliminaries

We let $e$ be a bilinear pairing function such that $e : \mathbb{G}_1 \times \mathbb{G}_2 \rightarrow \mathbb{G}_T$ . All groups have some prime-order $p$ . Let $\textmd{g}_1$ and $\textmd{g}_2$ be the generators for $\mathbb{G}_1$ and $\mathbb{G}_2$ respectively.

Next we define the hash function $H_1: \mathcal{M} \rightarrow \mathbb{G}_1$ . This function simply takes an arbitrary length message and maps it to an element of the $\mathbb{G}_1$ group.

BLS Signatures

BLS signatures $^{[1]}$ enable consensus proofs that are very efficient to verify as it supports both public key and signature aggregation. So a verifier only needs to verify a single aggregate signature rather than $n$ signatures.

$KeyGen():$ Choose a random $s \leftarrow \mathbb{F}_p$ and output $pk = \textmd{g}_2^s$ and $sk = s$

$Sign(sk, m):$ outputs $\sigma = H_1(m)^{sk}$ . This signature is a single group element in $\mathbb{G}_1$ .

$AggregateSignature(\sigma_1, \dots, \sigma_n) :$ This reduces a set of signatures $\sigma_1, \dots\sigma_n$ to a single group element $\tilde\sigma = \sum^{n-1}_{i=0}\sigma_i$ . Outputs $\tilde\sigma$ .

$AggregateKeys(pk_i, \dots, pk_n) :$ This reduces a set of public keys $pk_1, \dots, pk_n$ to a single group element $apk = \sum^{n-1}_{i=0}pk_i$ . Outputs $apk$ .

$Verify(pk, m, \sigma):$ Checks the equality of the pairing:

e(H_1(m)^{sk}, \textmd{g}_2) = e(H_1(m), pk)

This works because our pairing is bilinear:

e(H_1(m), \textmd{g}_2)^{sk} = e(H_1(m), \textmd{g}_2)^{sk}

This also extends to aggregate signatures:

\begin{equation} e(\textmd{g}_1, \tilde\sigma ) = e(apk, H_1(m)) \tag{1} \end{equation}

Homomorphic KZG Commitments

We’ve previously reviewed the KZG commitment scheme here. One great feature of KZG commitments is that they are homomorphic. What this means is that we can update the values in a commitment to some polynomial without needing the full polynomial. Recall that a KZG commitment $C$ to any set $V$ is of the form:

\textmd{g}^{\phi(s)} = \sum^{n}_{i=0} (\textmd{g}^{s^i})^{\phi_i}

Where $s$ is the secret value, $n = |V| - 1$ , and $\phi(x)$ is the polynomial that interpolates all the coordinates $(x_i, v_i)$ derived from the Lagrange basis:

\begin{split} \phi(x) &= \sum_{i \in [0, n)}^n v_i \cdot \mathcal{L}_i(x)\\ &= \sum_{i \in [0, n)}^n v_i \cdot (\prod\limits_{j \space = \space 1, \space \\ { i \space\ne \space j}}^{n} (\frac{x-x_j}{x_i - x_j})) \end{split}

Notice that we can rewrite our commitment $C$ as:

\textmd{g}^{\phi(s)} = \sum_{i \in [0, n)} (\textmd{g}^{\mathcal{L}_i(s)})^{v_i}

So that updating a value in this commitment from $v_i \rightarrow v_i^\prime$ can be seen as

\begin{equation} \textmd{g}^{\phi ^\prime (s)} = \textmd{g}^{\phi(s)} + (\textmd{g}^{\mathcal{L}_i(s)})^{\delta_i} \tag{2} \end{equation}

where $\delta_i$ is given as:

\delta_i = v^\prime_i - v_i\\

This works because:

\begin{split} \phi^\prime(x_i) &= \phi(x_i) + \mathcal{L}_i(x_i) \cdot \delta_i \\ &= v_i + \delta_i \\ &= v_i + v^\prime_i - v_i\\ &= v^\prime_i \end{split}

Unfortunately for the verifier, naively using equation $(2)$ to update it’s commitment requires computing the Lagrange base $\mathcal{L}_i(x)$ which has a runtime complexity of $O(2(deg(\phi)-1))$ . This complexity comes from evaluating the terms for both the numerator and denominator. An optimization that can be made here is to have the prover compute and provide the value $\textmd{g}^{\mathcal{L}_i(s)}$ instead, which the verifier can use to compute the update. But how can the verifier trust the correctness of this value? i.e $\mathcal{L}_i(x_i) = 1$ . This is where KZG proofs come in. First we define the polynomial $L(x)$ as the sum of all Lagrange bases in $\phi(x)$ :

L(x) = \sum^{n-1}_{i = 0} \mathcal{L}_i(x)

This allows us create a KZG commitment to this polynomial $\textmd{g}^{L(s)}$ as part of the KZG set up ceremony. Since we know that $L(x_i) - \mathcal{L}_i(x_i) = 0$ , thus the prover can compute a KZG proof for the $x_i$ -th coordinate using the quotient.

\psi(x) = \frac{L(x) - \mathcal{L}_i(x_i)}{(x - x_i)}

so that the verifier can verify $\textmd{g}^{\mathcal{L}_i(s)}$ by using the pairing check:

e(\frac{\textmd{g}^{L(s)}}{\textmd{g}^{\mathcal{L}_i(s)}}, \textmd{g}) = e(\textmd{g}^{\psi(s)}, \frac{\textmd{g}^s}{\textmd{g}^{x_i}})

But what if the prover wants to update multiple points in the commitment? Then they’ll have to submit the terms $(\textmd{g}^{\mathcal{L}_i(s)}, \textmd{g}^{\delta_i}) \space \forall i \in I$ where $I$ is the set of all points to be updated. So updating our commitments becomes

\begin{equation} \textmd{g}^{\phi ^\prime (s)} = \textmd{g}^{\phi(s)} + \sum^{|I|}_{i \in I}(\textmd{g}^{\mathcal{L}_i(s)})^{\delta_i} \tag{3} \end{equation}

What about verifying these terms? This is possible with KZG multi-proofs $^{[3]}$ . Dankrad's article on KZG commitments outlines that to verify batch KZG proofs, the verifier needs to compute some Lagrange bases themselves. However, the complexity for the bases is now reduced to $O(2(I - 1))$ . In our case, the prover has already supplied those Lagrange bases. Let's define $I(x)$ as follows:

I(x) = \sum^{|I|}_{i \in I} \mathcal{L}_i(x) \tag{4}

Using the polynomial in $(4)$ , We can come to the following conclusions:

\begin{align*} \forall i \in I, \space L(x_i) - I(x_i) &= 0 \\ L(x) - I(x) &= \psi(x) \cdot \prod^{|I|}_{i \in I} (x - x_i) \\ L(x) - I(x) &= \psi(x) \cdot Z_I(x) \end{align*}

Since the prover provides the individual terms $\textmd{g}^{\mathcal{L}_i(s)} \space \forall i \in I$ , the verifier can use them to compute:

\textmd{g}^{I(s)} = \sum^{|I|}_{i \in I}\textmd{g}^{\mathcal{L}_i(s)}

Finally the prover provides the KZG multi-proof $\textmd{g}^{\psi(s)}$ which is still a single group element, but allows us to verify multiple points using the pairing check:

e(\frac{\textmd{g}^{L(s)}}{\textmd{g}^{I(s)}}, \textmd{g}) = e(\textmd{g}^{\psi(s)}, \textmd{g}^{Z_I(s)}) \tag{5}

Casper FFG

The Casper FFG consensus protocol defines the finality rule for the Ethereum beacon chain $^{[4]}$ . It does this by introducing what it refers to as "source" and "target" checkpoints. These checkpoints are 32 slots apart and correspond to the epoch boundaries of the beacon chain. This means that Casper FFG finalizes whole epochs, rather than arbitrary block sequences.

An epoch according to the protocol goes through three stages: unjustified, justified, and finalized. The genesis block is a special case, as it is already finalized by the protocol rules. Moreover, an epoch (source) can only be considered finalized if there exists a direct descendant epoch (target) that has been justified by a supermajority of the authority set.

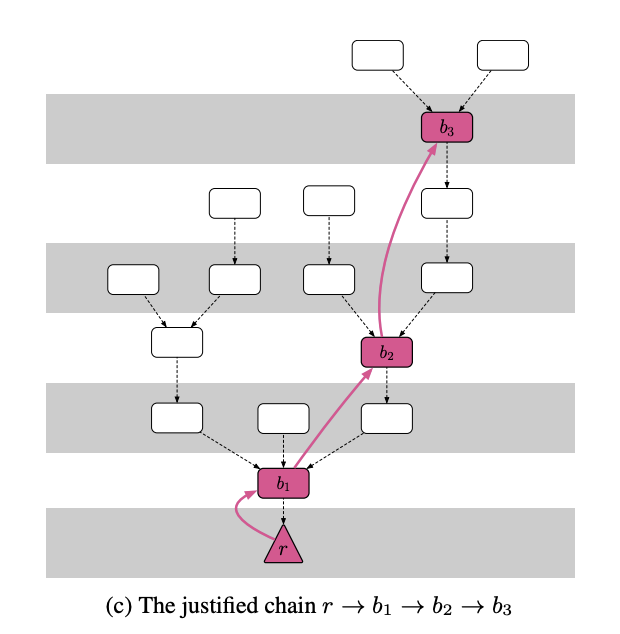
Blocks b1 & b2 are finalized, while b3 is only justified.

As stated in my article on the sync committee, there are simply too many authorities in the Ethereum beacon chain (Currently 560k and rising). Passing around a epoch checkpoint to sign would degrade the network. To solve this issue, the authorities are split up into committees with a maximum count of 2048 per committee. These attestation committees produce signed Casper FFG votes. The Casper FFG protocol uses BLS signature which allows signatures from individual committee members to be aggregated into a single signature per committee.

Attestation messages are published in the beacon chain blocks and contains: Casper FFG votes, a bitlist of the validators in the committee who signed the attestation and a BLS signature over the AttestationData. The BLS signatures for the attestation messages use the $\mathbb{G}_1$ group for public keys, while it’s signatures are in the $\mathbb{G}_2$ group. A consensus client observing the attestation messages can conclude that some epoch is justified (and it’s parent finalized) if they collect enough messages from a supermajority of the validator set confirming the epoch.

struct Attestation {
    aggregation_bits: Bitlist<MAX_VALIDATORS_PER_COMMITTEE>
    data: AttestationData
    signature: BlsSignature
}
 
struct AttestationData {
    slot: u64
    index: u64
    // LMD GHOST vote
    beacon_block_root: H256
    // FFG vote
    source: Checkpoint
    target: Checkpoint
}

Validators can join the validator set by locking up 32 ETH. The beacon chain adds their BLS public key as well as other protocol metadata (such as their activation_epoch, exit_epoch and a boolean flag that tracks if they’ve been slashed ) to the “validator registry” an ssz list object on the [BeaconState](https://github.com/ethereum/consensus-specs/blob/dev/specs/phase0/beacon-chain.md#beaconstate) . Once added to the validator set, their initial activation_epoch and exit_epoch is set to a constant FAR_FUTURE_EPOCH $(2^{64}-1)$ [source]. This triggers the epoch transition function to schedule them for activation for the next epoch once the current epoch ends. [source]. It's worth noting that the beacon chain does NOT remove any validators from its registry. Instead, it updates their activation_epoch, exit_epoch, or slashed values.

If a validator is found to have either proposed two competing beacon blocks for the same height [source] or signed an attestation that violates casper FFG's rules [source]. Then their validator.slashed will be updated to true immediately, meaning they can no longer propose blocks or sign attestations. Validators may choose to voluntarily exit the active set after some minimum period, after which their exit_epoch will be changed from FAR_FUTURE_EPOCH to some near future epoch. [source]. Hence, all inactive validators will satisfy the condition exit_epoch < current_epoch < activation_epoch or slashed = true.

It is critical to note that both the BeaconState and the "validator registry" list are SSZ objects that can be merkleized. As a result, it is possible to obtain SSZ merkle multi-proofs of validator state changes, such as deposits (new deposits), exits, and slashings, which can be verified against the BeaconState root. This will be important later on.

Aggregate Public Key Proofs

The Accountable Light Client Systems for PoS Blockchains $^{[5]}$ paper by Web3 Foundation researchers presents a SNARK that can verify whether the constituent public keys in an aggregate BLS public key exist as a subset of a list of potential signers. Using this SNARK the verifier only needs to maintain a KZG commitment to the BLS public keys of all potential signers.

More formally, Given a set of potential signers $\{pk_i\} \forall i \in$ $T$ . The verifier holds a commitment $C$ to the list of public keys in $T$ . The prover can then send a bitlist $b$ which represents a subset $S$ of the signers in $T$ , an aggregate BLS signature $\sigma$ , aggregate public key $apk = \sum_{i = 0}^{|S|} pk_i$ and a succint proof $\pi$ that $apk = \sum_{i = 0}^{|T|} b_i \cdot pk_i$ .

After verifying the aggregated public key SNARK proof $\pi$ , the verifier can simply perform the naive aggregate BLS signature verification. This SNARK construction removes the requirement for the verifier to know the individual public keys in $T$ making it perfect for truly light clients.

The SNARK circuit itself simply performs elliptic curve affine additions of the BLS public keys and constrains these additions using a custom PLONK gate.

Screenshot 2023-05-10 at 11.52.59 AM.png

The SNARK requires a pair of pairing-friendly elliptic curves: one for the BLS signature (the inner curve) and one for the SNARK itself (the outer curve). The paper recommends using the curves BLS12-377 and BW6-761. However, for the BLS12-381 keys used in the Casper FFG protocol, we must use the BW6-767 curve for the outer curve to avoid non-native field arithmetic that would significantly increase the number of constraints and, consequently, proving times. The protocol for aggregated public key proofs is formally defined below:

$APK.Setup(t, s):$ This outputs the proving and verification keys $\langle srs_{pk}, srs_{vk} \rangle$ using the powers of $s$ and a SNARK preprocessing algorithm, which can be used to commit and prove a maximum number of $t$ signers.

$APK.Commit(srs_{pk}, T):$ Given a set of public keys $T = \{pk_i\}_{i = 1}^{t}$ , outputs a commitment to the public keys $C$ .

$APK.Prove(srs_{pk}, C, \{pk_i\}^{|S|}_{i = 1}, b):$ Computes the SNARK proof for the aggregation of the given public keys and a bitlist $b = \{bit_i\}^t_{i = 1}$ that indicates their positions in the original set $T$ . Outputs $\pi_{apk}$ .

$APK.Verify(srs_{vk}, C, apk, \pi_{apk}, b):$ Given the commitment, aggregated public key, SNARK proof and bitlist. This verifies that $apk = \sum_{i = 0}^{|S|} b_i \cdot pk_i$ . Outputs $1/0$ .

Protocol

With the preliminaries out of the way, let's take a look the zkCasper protocol. Our approach is to begin by establishing a trusted commitment to the list of all validators in the Beacon chain. However, the validators in the Beacon chain will not sign this commitment as the statuses of the individual validators in the set changes. Instead, they sign the block roots of epoch boundaries. Fortunately, these block roots contain a merkle commitment to all the validators in the validator registry. Therefore, the verifier can leverage the homomorphic property of KZG commitments in order to update their commitment after verifying the merkle proofs of the validator set changes. In this way, the verifier can securely track all validator set changes.

Armed with this commitment, the verifier only needs to know the aggregate of public keys that signed a committee's attestation messages. Using the apk SNARK, the verifier can confirm that the aggregate of these aggregate public keys, along with a bitlist and a SNARK proof, corresponds to the commitment it has to the public keys of the full validator set. This enables the verifier verify as many attestation messages at once in order to take advantage of the performance benefits of equation $(1)$ .

An issue that arises is that the beacon chain uses a combination of Casper FFG and LMD Ghost $^{[6]}$ . A consequence of this decision is that signed attestations do not need to reach super-majority participation before they are published in beacon chain blocks. This means that there may be multiple signed attestation messages from a committee with overlapping participants. The aggregate of these overlapping signers is unfortunately incompatible with the apk SNARK’s constraints. However this just means we cannot verify a supermajority of the beacon chain’s attestations in one go, we can instead prove $n$ batches of attestations that have no overlapping committee signatures. Where $n$ is the maximum number of times a single committee produced an attestation.

The protocol is formally defined below:

$Setup(s, t, V):$ Performs the SNARK set up, $\langle srs_{pk}, srs_{vk} \rangle \rarr APK.Setup(t, s)$ . Computes the commitment $C = APK.Commit(srs_{pk}, V)$ where $V$ is the set of all validator public keys. Computes the update key $srs_{uk} = g^{L(s)}$ . Outputs $\langle srs_{uk}, srs_{pk}, srs_{vk} \rangle$ .

$ProveAttestations(srs_{pk}, C, A):$ Given a set of $n$ Casper FFG committee attestations with non-overlapping signatures $A = (m_i, \tilde\sigma_i, (\{pk_j\}^{|P|}_{j=1})_i) \forall i \in [1, n)$ where $P$ is the set of participating public keys in each committee attestation. The prover computes the bitlist $b$ for the participating public keys of all the individual validators, then finally they compute the apk proof for the aggregation of these public keys, and outputs $\langle A, \pi_{apk}, b \rangle$ . Where:

\pi_{apk} = APK.Prove(srs_{pk}, C, \sum^{|P| \cdot n}_{i=1} pk_i , b)

$VerifyAttestations(srs_{vk}, C, A, S, \pi_{apk}, b):$ Where, $A = (m_i, \tilde\sigma_i, apk_i) \forall i \in [1, n)$ , $m_i = \langle \mathcal{E}_s, \mathcal{E}_t \rangle$ . First the verifier computes $b = d \oplus b$ , where $d$ is the bitlist of disabled validators, next they verify the apk proof for the participating public keys:

APK.verify(srs_{vk}, C, \sum^n_{i=0} apk_i , \pi_{apk}, b) \in \{true, false\}

finally they verify the BLS signatures for each committee’s attestations using equation $(1)$

e(\textmd{g}_1, \tilde\sigma_i ) = e(apk_i, H_1(m_i))

If all signature verifications pass, the verifier updates the bitlist for all the signers seen so far by computing $S = S \lor b$ . Outputs $1/0$ . A source epoch boundary $\mathcal{E}_s$ should be considered final if $Hamming(S) \ge \frac{2}{3}(|C| - |d|) + 1$ .

$ProveValidatorUpdates(C, I, srs_{uk}):$ The prover computes the merkle multi-proof $\pi_{merkle}$ for all validators $v_i \in I$ whose status (joined, exit_epoch, activated_epoch, slashed) have changed with respect to the latest finalized epoch block root $\mathcal{E}_s$ . Next they compute the KZG proof $\pi_{kzg} = g^{\psi(s)}$ for the points that pass through $I(x)$ defined in $(4)$ . Outputs $\langle I, \pi_{kzg}, \pi_{merkle} \rangle$ .

$UpdateValidatorSet(srs_{uk}, C, I, \pi_{merkle}, \pi_{kzg}, \mathcal{E}_s) :$ First the verifier verifies the ssz merkle proof for the validator statuses via $ssz.Verify(\mathcal{E}_s, \pi_{merkle}, \{v_i \space \forall i \in I\})$ , where $v_i$ represents the validator struct in the beacon state for the block root of the finalized epoch $\mathcal{E}_f$ . If the Merkle verifications pass, the verifier then proceeds to verify $I(x), \pi_{kzg}$ using the equation in $(5)$ . If the KZG proof is valid, then the verifier can update their commitment $C$ with the set of all new validators in $I$ using equation $(3)$ . Finally they compute $d = (d \lor r) \oplus a$ , where $r, a \sub I$ , $r$ is the bitlist of all validators who have been disabled (exited, slashed) and $a$ is the bitlist of all validators who have been activated. Outputs the updated commitment $C^{\prime}$ .

References

$^{[1]}$ Dan Boneh; Ben Lynn & Hovav Shacham. "Short Signatures from the Weil Pairing".

$^{[2]}$ Dan Boneh, Manu Drijvers, and Gregory Neven. "Compact Multi-Signatures for Smaller Blockchains"

$^{[3]}$ Dankrad Feist, Kate Polynomial Commitments

$^{[4]}$ Vitalik Buterin and Virgil Griffith. "Casper the Friendly Finality Gadget"

$^{[5]}$ Oana Ciobotaru, Fatemeh Shirazi, Alistair Stewart , and Sergey Vasilyev. "Accountable Light Client Systems for PoS Blockchains"

$^{[6]}$ Combining Ghost and Casper